

Starts with 1, then 1, then you add the prior 2 together and keep on going in that sequence:
According to James Nickel, author of Mathematics: Is God Silent?, the Fibonacci Sequence is related to the petal arrangement of flowers; is found in the spiral arrangements of petals, pine cones, and pineapple; in the leaf positioning of the Phyllotaxis, in the mathematics of the quantum matrix, of rabbit populations, and of the genealogy of male bees.
The Fibonacci Sequence shows up in the musical octave as shown below:
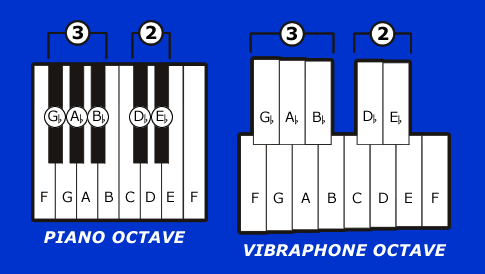
There are
2 black keys, then
3 black keys, totalling
5 total black keys.
8 white keys make the octave.
13 keys total.
2, 3, 5, 8, 13 is a subset of the Fibonacci Sequence.
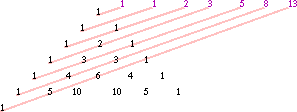
Pascal's Triangle, which is used to solve binomials and probability is related to the Fibonacci Sequence as shown below:
If you look at the Fibonacci Sequence and divide, you will find a trend. If you divide one number by the number before it
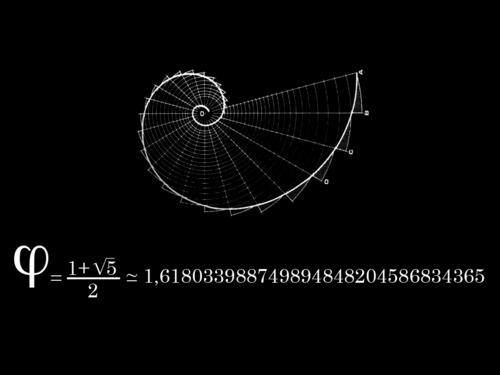
continuously, the result approaches ![]() (Phi) which is about equal to 1.618033989.
See below:
(Phi) which is about equal to 1.618033989.
See below:
In fact, you can choose any 2 numbers and this will work. Say I choose 8 and 26 and form a Fibonacci-like Sequence as such:
Now say I seek Phi using the same dividing method mentioned above. I get the following:
The result approaches Phi. Amazing!
The Golden Rectangle, whose ratio of the longer side to the shorter side is the value of Phi (also called the Golden Ratio) also contains a spiral that is seen in the cochlea of the human ear, the chambered nautilus, the spiral galaxy, and in hurricane storm clouds according to James Nickel, author of Mathematics: Is God Silent?. Further, the proportions of the Golden Rectangle have been used in art and architecture. More information about the Golden Rectangle.
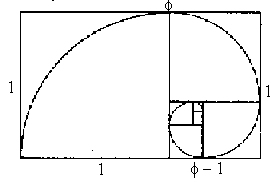
The shorter side is 1 and the longer side is ![]() (Phi).
(Phi).
James Nickel explains in his book Mathematics: Is God Silent? how Phi relates to the
Pentagram/Pentagon of 5-petaled flowers, starfish, and sand dollars.
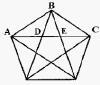
In the figure above AC/AB = ![]() .
.
|
1/ Solving for |
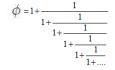
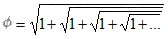 and if you add it to 1, you get |
 |
 Click to Zoom |
 Click to Zoom |
 |
Cool Math - lessons, games and more!




Sator Square:
| S | A | T | O | R |
| A | R | E | P | O |
| T | E | N | E | T |
| O | P | E | R | A |
| R | O | T | A | S |
The Sator Square may be read top-to-bottom, bottom-to-top, left-to-right, and right-to-left: SATOR AREPO TENET OPERA ROTAS. Translation from Latin: The sower Arepo has work of wheels; that is, the farmer uses his plough for his work.

































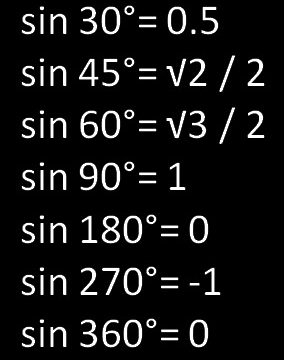


















Algebra at The Free Information Society (web archive)
Calculus at The Free Information Society (web archive)
Circle - Radians, Degrees and Coordinates
Curves and Equations Reference
Doodling in Math Class: Spirals, Fibonacci, and Being a Plant - Part 1
Doodling in Math Class: Spirals, Fibonacci, and Being a Plant - Part 2
Doodling in Math Class: Spirals, Fibonacci, and Being a Plant - Part 3
Glimmers of Light from the Eye of a Giant (web archive)
The Golden Ratio - a sacred number that links the past to the present | Ancient Origins
Golden Spiral on squareCircleZ
The Greatest Mathematicians of All Time
Hero of Alexandria at Wikipedia
Math Articles at The Free Information Society (web archive)
The Mathematical Association of America
The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics
Where's the Math? (web archive)